HF 2 (15 pont)

• Minden feladatot a feladatszámnak megfelelő számú megoldásnotebookban oldj meg. Az első feladatot az feladat01.ipynb notebookban és így tovább.
• A megoldás tartalmazza a megoldandó feladat szövegét a megoldásnotebook első markdown cellájában!
• A beadott notebookok letisztázottak és igényesen szerkeztettek legyenek!
• Kommentekkel, illetve markdown cellákkal magyarázd, hogy éppen mit csinál az adott kódrészlet!
• Magyarázat nélkül a beküldött feladatok AUTOMATIKUSAN 0 PONTOT ÉRNEK!
• Az elkészített ábrák minden esetben rendelkezzenek ábrafeliratokkal (cím, tengelyfeliratok és − amennyiben indokolt − jelmagyarázat)! Amennyiben a beadott ábrákon nincsenek feliratok, az adott feladat AUTOMATIKUSAN 0 PONTOT ÉRNEK!
• A beadott notebookok Kernel -> Restart&Run All hatására a beadott formát reprodukálják! (Próbáld ki!)

---

Feladat 1 (2.5 pont)

Vizsgáljuk az alábbi testek szomszédsági mátrixait!

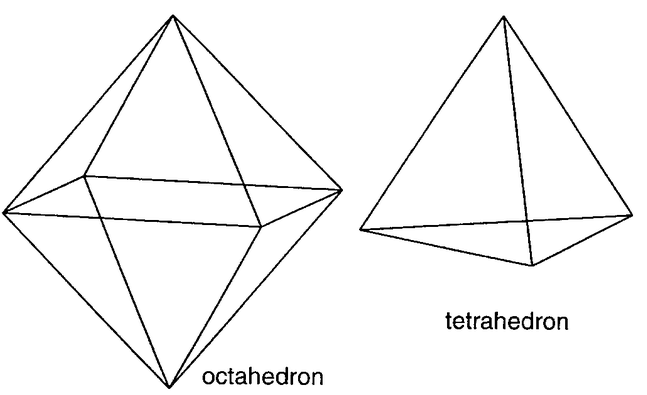
• Hatarozd meg az ábrán látható gráfok szomszédsági mátrixát! A szomszédsági mátrixban minden a sima vonallal jelölt összeköttetéseknél a mátrix elem legyen 1.(0.5p)

• Ismeretes, hogy bármely háromszögekből álló $G$ gráfhoz tartozó $A$ szomszédsági mátrix hatványainak nyomával kifejezhetőek a gráf éleinek $e$ száma illetve a gráfot allkotó háromszögek $t$ száma az alábbiak szerint (lsd: az alábbi cikket): $$ \mathrm{tr}{(A^2)} = 2e $$ $$ \mathrm{tr}{(A^3)} = 6t $$

• Felhasználva a fenti összefüggéseket -- és azt a tényt, hogy a fenti poliédereket kizárólag háromszögek határolják --, írj egy függvényt (legyen a neve Euler), mely bemeneti paramétere az adott gráf $A$ szomszédsági mátrixa, és ellenőrzi az Euler-féle poliédertételt! A függvény visszatérési értéke legyen a topologikus invariáns -- mely ebben az esetben 2 -- és True vagy False függően attól, hogy teljesül-e vagy nem! (0.75p)

• Számítsuk ki mindkét fentebb kapott mátrix összes permutációs mátrixát! A python beépített itertools moduljának permutations függvénye segítségedre lehet. Bővebb információt itt találsz. (0.5p)
• Igazold numerikusan mindkét esetre, hogy tetszőleges $P$ permutáció esetén az $A_2 = P^TAP$ transzformációval kapott mátrix spektruma megegyezik az eredeti $A$ szomszédsági mátrix spektrumával! (0.5p)

Feladat 2 (2.5 pont)

Vegyük a következő $n$ dimenziós mátrixokat: $$M=\begin{pmatrix} Q&k&k&\dots&k\\ 1&Q&k&\dots&k\\ 1&1&Q&\dots&k\\ \vdots&\vdots&\vdots&\ddots&\\ 1&1&1&&Q \end{pmatrix}$$

• Hozz létre egy függvényt, aminek 3 bemeneti paramétere $n$, $Q$, és $k$, ami legenerál egy, a fenti struktúrával rendelkező $n\times n$ dimenziós mátrixot. A függvényben ne használj for ciklust. (0.5p)
• A függvény segítségével generáld le $k=2$, $Q=2$ paraméterekkel az n=2 dimenziós mátrixot. Számold ki a mátrix sajátvektorait, majd azok első komponensét oszd el a másodikkal. Mit tapasztalsz? (0.25p)

Vegyük a következő összefüggést: $c(l)=M^lc(0)$. Legyen $M$ az előző feladatrészben is használt mátrix, és $c(0)=\begin{pmatrix}1\\1\end{pmatrix}$

• Ábrázold $c(l)$ első komponensének a második komponensel vett hányadosát a $l$ függvényében, $l\in\left[0,10\right]$ tartományon. Mit tapasztalsz? (0.5p)
• Hasonlóan az előző feladatrészhez, ugyanezt ábrázold három különböző mátrixra, amik paraméterei $n=2$, $k=3$, $Q=\{1,1.7,2\}$ paraméterekre. Ábrázolás előtt a kapott értékekből vonj ki $\sqrt{3}$-at, vedd az abszolút értékét, és logaritmikus skálán legyen az y tengely. Melyik $Q$ paraméterre lesz a leggyorsabb a lecsengés? (0.5p)
• Mi történik ha $Q=\sqrt{k}$? Elég egy lépésig vizsgáld.(0.25p)

Vizsgáljuk meg n>2 esetet. Legyen n=20, k=2, és Q=0. A valós sajátértéket elhagyva ábrázold a mátrix sajártértékeit. Az x tengelyen legyen a valós, y tengelyen a képzetes része. (0.5p)

Feladat 3 (2.5 pont)

Definialjuk az $I$, $X$, $Y$ és $Z$ 2x2-es mátrixokat az alábbi módon:

\begin{align} I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} && X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} && Y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} && Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}. \end{align}

A fentebbi mátrixok és a mátrixok között definiált Kronecker szorzat ($\otimes$) segítségével definiáljuk a következő $2N$ darab mátrixot \begin{align} a_k &= \underbrace{Z \otimes Z \otimes \cdots \otimes Z}_{k - 1} \otimes \frac{X + i Y}{2} \otimes \underbrace{ I \otimes \cdots \otimes I}_{N - k}\\ a^\dagger_k &= \underbrace{Z \otimes Z \otimes \cdots \otimes Z}_{k - 1} \otimes \frac{X - i Y}{2} \otimes \underbrace{ I \otimes \cdots \otimes I}_{N - k},\end{align} ahol $k \in \{1, 2, \ldots, N\}$. A $\otimes$ bináris operátor definíciójáról és tulajdonságairől itt olvashatsz: https://en.wikipedia.org/wiki/Kronecker_product.

Írj egy függvényt aminek a neve fermion_op! A függvény viselkedjen a következő módon:

• A függvény bemenő paraméterei legyenek a $k$ és $N$ egész számok, továbbá egy bool típusú változó aminek legyen a neve dagger! (0.25p)

• Ha dagger értéke False térj vissza a fentebb definiált $a_k$ mátrixal. Ha pedig dagger értéke True térj vissza az $a^\dagger_k$ mátrixal! (0.75p)

• A függvény visszatérési értéke legyen egy ritka mátrix és Kronecker-szorzatok kiszámolásához használd a SciPy csomag scipy.sparse.kron függvényét! (0.5p)

A fermion_op függvény segítségével

• Ellenőrizd le a következő mátrix azonosságokat $a_k a_l + a_l a_k = 0$ az $N = 5$ esetben, ahol $k,l \in \{1, 2, \ldots, N\}$! (0.5p)

• $N$ függvényében határozd meg $a_k$-nak a nem nulla mátrixelemeinek számának arányát az összes mátrixelem számához képest (elég egy tetszőleges $k$-ra megcsinálni)! Ábrázold az eredményt $N$ függvényében a $[3, 15)$ tartományon! (0.25p)

• Saját szavaiddal fogalmazd meg érdemes volt-e ritka mátrixokat használni? (0.25p)

Feladat 4 (2.5 pont)

Ebben a feladatban inhomogén alakzatok tehetetlenségi nyomatékát fogjuk meghatározni numerikus számítások segítségével. Egy $\rho(x,y)$ sűrűségeloszlással jellemezhető test tömegközéppontja definíció szerint $$\mathbf{r}_\text{CM} = \frac{\int \mathbf{r} \cdot \rho(x, y) dV}{\int \rho(x, y) dV}.$$ A tömegközéppontra vonatkoztatott tehetetlenségi nyomaték tenzor (ami jelen esetben egy $2\times 2$-es mátrix) pedig: $$ \Theta = \int \rho(x, y) \left[|\mathbf{r} - \mathbf{r}_\text{CM}|^2 \cdot \mathbb{1} - (\mathbf{r} - \mathbf{r}_\text{CM}) \circ (\mathbf{r} - \mathbf{r}_\text{CM})\right] dV $$ ahol $\mathbb{1}$ a $2\times 2$-es egység mátrix és $\circ$ a diadikus szorzatot jelöli az inegrálási változó $\mathbf{r}$ Descartes-komponensei: $$\mathbf{r} = \begin{pmatrix} x \\ y \end{pmatrix}$$

Vizsgáljuk az alábbi két alakzatot:

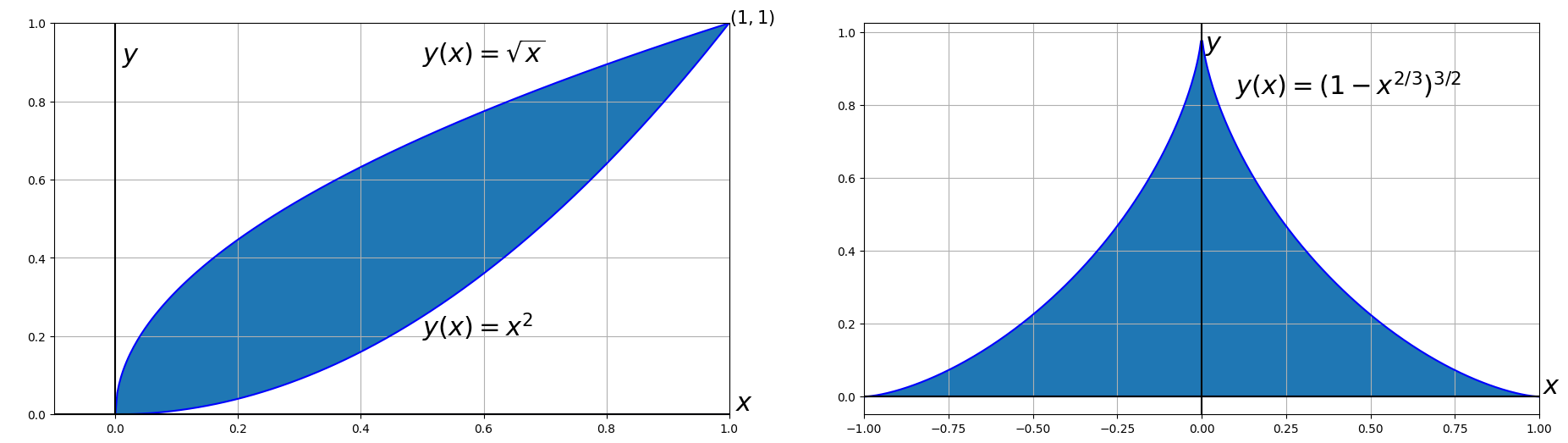
a) Az $y = \sqrt{x}$ és az $y = x^2$ görbék által határolt alakzatot melynek a sűrűsége a következő: $\varrho(x,y)=10e^{-x^2}+y.$

• Határozd meg a tömegközéppont koordinátáit! (0.5p)
• Számold ki a tehetetlenségi nyomaték tenzort a tömegközéppontban, majd diagonalizáld is azt! (0.5p)
• Készíts ábrát melyen feltűnteted az alakzatot, a tömegközéppontot és a tehetetlenségi nyomaték tenzor sajátvektorait melyek az alakzat főtengelyét adják. (0.25p)

b) Egy asztroid alakú testet, melynek a sűrűsége pontról, pontra változik a következő összefüggés szerint: $\varrho(x,y) = xy+e^{-y^2}.$

• Határozd meg a tömegközéppont koordinátáit! (0.5p)
• Számold ki a tehetetlenségi nyomaték tenzort a tömegközéppontban, majd diagonalizáld is azt! (0.5p)
• Készíts ábrát melyen feltűnteted az alakzatot, a tömegközéppontot és a tehetetlenségi nyomaték tenzor sajátvektorait melyek az alakzat főtengelyét adják. (0.25p)

Az integrálást mindent esetben Descartes-koordinátarendszerben végezzük el a scipy modul kettős integrálást implementáló függvénye segítségével. A határok megállapításában segítenek az ábrák!

Feladat 5 (2.5 pont)

Vizsgáljuk meg az egyik legismertebb kaotikus rendszer, a kettős inga mozgását. A kettős ingát leíró differenciálegyenlet felírásához el kell hagyjuk a Descartes-i koordinátát, és át kell térünk egy olyan rendszerbe, ahol a függőlegestől való $\theta$ szöggel, és ennek $\omega$ szögsebességével írjuk le a kettő összecsatolt tömegpontunkat pontunkat.

Ahogy az ábrán is látható, a kettős inga paraméterei az $l_1$, $l_2$ hosszok, $m_1$, $m_2$ tömeg és a $g$ gravitációs gyorsulás. A differenciálegyenletek felírásához vezessünk be négy segédfüggvényt: $$a_1(\theta_1,\theta_2) = \frac{l_2}{l_1}\left(\frac{m_2}{m_1+m_2}\right)\cos\left(\theta_1 - \theta_2\right)$$ $$a_2(\theta_1,\theta_2) = \frac{l_1}{l_2}\cos\left(\theta_1 - \theta_2\right)$$ $$f_1(\theta_1,\theta_2,\omega_1,\omega_2) = - \frac{l_2}{l_1}\left(\frac{m_2}{m_1+m_2}\right)\omega_2^2\sin\left(\theta_1 - \theta_2\right)-\frac{g}{l_1}\sin\theta_1$$ $$f_2(\theta_1,\theta_2,\omega_1,\omega_2) = \frac{l_1}{l_2}\omega_1^2\sin\left(\theta_1 - \theta_2\right)-\frac{g}{l_2}\sin\theta_2$$ Ezek segítségével a megoldandü differenciálegyenleteket az alábbi egyszerű alakra tudjuk hozni: $$\ddot{\theta_1} = \frac{f_1-a_1f_2}{1-a_1a_2}$$ $$\ddot{\theta_2} = \frac{-a_2f_1+f_2}{1-a_1a_2}$$

• Írd meg a segédfüggvényeket. (0.5p)
• Írd meg a mozgásegyenlet növekmény függvényét. (0.5p)

Legyenek a paraméterek a következők: $m_1 = m_2 = 1$, $l_1=l_2=1$ és $g=1$. Ezen paraméterek mellett numerikusan integráljuk a mozgásegyenletet 9 különböző kezdeti feltétellel: $$\theta_1 = \pi/2 + \{-0.01,0,0.01\}$$ $$\theta_2 = \pi/2 + \{-0.01,0,0.01\}$$ $$\omega_1=\omega_2=0$$

• A $\theta_1$ és $\theta_2$ minden lehetséges kombinációjával integráljuk ki a mozgásegyenletet $t=60$-ig. (1p)
• Ábrázold egy ábrán mind a kilenc kezdőfeltétel esetén $\theta_1$-et $t$ függvényében. Mit tapasztalsz? (0.5p)

Feladat 6 (2.5 pont)

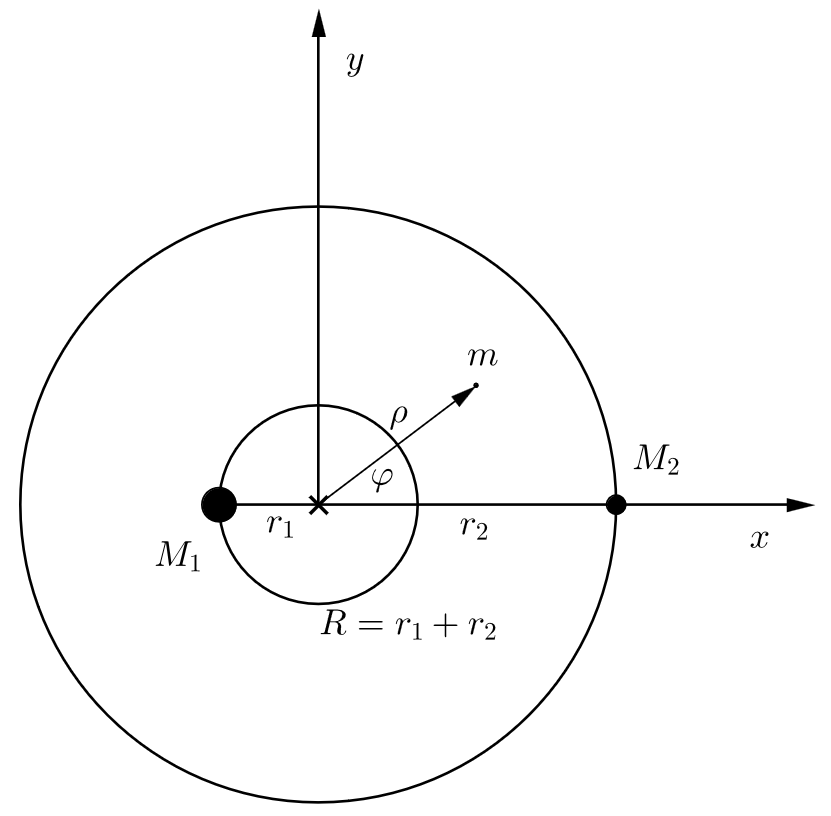
Az alábbi differenciál egyenletek írják le egy kis tömeg mozgását két nagyobb tömeg jelenétében amik egymás körül keringenek. Ehhez feltételeztük, hogy a három test egy síkban kering. Legyen a koordináta rendszerünk közepe a rendszer tömegközéppontja és jelöljük $\rho$-val és $\varphi$-vel a kis tömeg polárkoordinátáit.

\begin{align*} &\dot{p}_\rho = \frac{p_\varphi^2}{\rho^3} - \frac{\mu_1\left(\rho + r_1 \cos\varphi\right)}{\sqrt{\rho^2 + r_1^2 + 2r_1 \rho \cos \varphi}^3} - \frac{\mu_2\left(\rho - r_2 \cos\varphi\right)}{\sqrt{\rho^2 + r_2^2 - 2r_2 \rho \cos \varphi}^3},\\ &\dot{p}_\varphi = \sin \varphi \left(\frac{\mu_1 \rho r_1}{\sqrt{\rho^2 + r_1^2 + 2 r_1 \rho \cos\varphi}^3} - \frac{\mu_2 \rho r_2}{\sqrt{\rho^2 + r_2^2 - 2 r_2 \rho \cos\varphi}^3}\right), \\ &\dot{\rho} = p_\rho \vphantom{\frac{1}{2}}, \\ &\dot{\varphi} = \frac{p_\varphi}{\rho^2} - \omega, \end{align*}

ahol \begin{align*} \mu_i = G M_i && \omega = \sqrt{8\frac{\mu_1 + \mu_2}{R^3}} && r_1 = \frac{\mu_2 R}{\mu_1 + \mu_2} && r_2 = \frac{\mu_1 R}{\mu_1 + \mu_2} \end{align*}

A továbbiakban dolgozzunk a $\mu_1 = G M_2 = 1$ és $R = 1$ mértékegység rendszerben és legyen $\mu_2 = \frac{1}{81}$. A kezdeti feltétel pedig legyen $t = 0$-ban \begin{align*} \rho(0) = 1.17 r_2, && \phi(0) = 0, && p_\rho(0) = 0, && p_\varphi(0) = 0.7. \end{align*}

• Írj egy python függvényt mely implementálja a fenti differenciálegyenlet rendszer növekményfüggvényét(1.0p)!
• Integráld a differenciálegyenlet rendszert a $[0, 8]$ intervallumon a fent megadott kezdőfeltétel mellett. (1.0p)
• Ábrázold a megoldást pályáját, az ábrán tüntestd fel a másik két nagytömegű test pozícióját is. (0.25p)
• A saját szavaiddal fogalmazd meg, hogy a mozgás alakja jól közelíthető-e Kepler-pályával. (0.25p)