HF 1 (15 pont)¶

Minden feladatot a feladatszámnak megfelelő számú megoldásnotebookban oldj meg. Az első feladatot az feladat01.ipynb notebookban és így tovább.
A megoldás tartalmazza a megoldandó feladat szövegét a megoldásnotebook első markdown cellájában!
A beadott notebookok letisztázottak és igényesen szerkeztettek legyenek!
Kommentekkel, illetve markdown cellákkal magyarázd, hogy éppen mit csinál az adott kódrészlet!
Magyarázat nélkül a beküldött feladatok AUTOMATIKUSAN 0 PONTOT ÉRNEK!
Az elkészített ábrák minden esetben rendelkezzenek ábrafeliratokkal (cím, tengelyfeliratok és − amennyiben indokolt − jelmagyarázat)! Amennyiben a beadott ábrákon nincsenek feliratok, az adott feladat AUTOMATIKUSAN 0 PONTOT ÉRNEK!
A beadott notebookok Kernel -> Restart&Run All hatására a beadott formát reprodukálják! (Próbáld ki!)

Feladat 1 (2.5 pont)¶

A kombinatorikai feladatok megoldása során gyakran találkozhatunk a Catalan-számokkal. Ezen egész számok az alábbi rekurziós összefüggést elégítik ki:

$$ \displaystyle C_{0}=1\quad {\text{and}}\quad C_{n}={\frac {2(2n-1)}{n+1}}C_{n-1}\quad {\text{for }}n>0. $$

A Catalan-számok egyik érdekes tulajdonsága, hogy a belőlük alkotott Hankel-mátrixok determinánsa garantáltan 1.

Az alábbi részfeladatok implementációja során külső modulok függvényeit ne használd! Amennyiben a definíciókban külső, például numpy, vagy scipy rutinok vannak, a teljes feladatod automatikusan 0.0 pontot ér.

Írj egy függvényt, melynek a neve legyen MCn! A függvényednek egyetlen bemenő paramétere legyen, n, mely egy egész szám! A függvény visszatérési értéke egy listákat tartalmazó lista legyen, ami a Catalan-számokat tartalmazó $n\times n$-es Hankel-mátrix(0.5p)!$\newline$ Például $n=4$ esetén az alábbi kimenetet produkálja a függvény:
```
>>> MCn(4)

[[1, 1, 2, 5],
[1, 2, 5, 14], 
[2, 5, 14, 42], 
[5, 14, 42, 132]]
```

Egy mátrix determinánsa megadható a mátrix egész számú hatványainak spúrjának (nyomának vagy traceének) segítségével az alábbi rekurziós formula segítségével: $$ \displaystyle b_{n}=1;~~~b_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}b_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n) $$ $$ \mathrm{det}(A) = (−1)^nb_0 $$

Implementáljuk a fenti kifejezést egy tetszőleges $n \times n$-es mátrixra, úgy, hogy a mátrixelemeket mint list-ek list-jei tároljuk!

Írj egy függvényt, melynek neve legyen mp! Rendelkezzen két bemenő paraméterrel, A-val illetve B-vel, melyek két ugyan olyan méretű mátrix mátrixelemeit tartalmazzák (mint list-ek list-jei)! A függvény kimenete pedig a két mátrix szorzat mátrixa legyen (mint list-ek list-jei), azaz a kimeneti mátrix elemeire teljesüljön a szokásos $ \displaystyle C_{ij}=\sum_k A_{ik}B_{kj}$ kifejezés (0.25p)!
Írj egy függvényt, melynek neve legyen pow_traces, melynek egy bemenő paramétere van, mely egy A $n\times n$-es mátrix (melynek elemei mint list-ek list-jei vannak tárolva)! A függvény kimenete pedig egy $n$ elemű list legyen, melynek elemei a mátrix első $n$ hatványának a spúrjai! Például, ha A a fent kiírt MCn(4) mátrix, akkor a függvény kimenete az alábbi listát kell, hogy produkálja (0.5p):
```
>>> pow_traces(MCn(4))
[149, 21655, 3186149, 468835855]
```
Készíts egy függvényt det néven, amelynek egyetlen bemeneti paramétere van, ez pedig egy $n \times n$-es mátrix (A). A mátrix elemeit list-ek list-jében tároljuk. A függvény kimenete legyen az A mátrix determinánsa! A determináns meghatározásához implementáld a fent megadott rekurziós kifejezést! A függvényed támaszkodjon a korábban definiált mp és pow_traces függvényekre (0.5p)!

Használd a korábban definiált függvényeket egy ábra létrehozásához, amelyen $1 \leq n \leq 9$ tartományban ábrázolod a Catalan-számokat tartalmazó Hankel-mátrixok determinánsát az $n$ dimenzióban. Az ábra elkészítésénél alkalmazd a matplotlib modul megfelelő függvényeit! (0.5p)!
A saját szavaiddal diszkutáld a kapott ábra eredményeit! Azt kaptad amire számítottál? Ha nem, akkor diszkutáld az esetlegesen felmerülő hibalehetőségeket (0.25p)!

Feladat 2 (2.5 pont)¶

Ebben a feladatban a python beépített time moduljával ismerkedünk meg. Segítségével rávilágítunk arra, hogy miért célszerű, ahol lehet, a numpy rutinjait alkalmazni egyszerű matematikai formulákkal definiálható adatok generálásához és manipulálásához.

Egy markdown cellában a saját szavaiddal, legalább 5-6 mondatban, fogalmazd meg, hogy a python time modulja segítségével hogyan tudod megmérni egy adott kódrészlet futtatásához szükséges időt! Ahol szükséges ott a források megjelölésével hivatkozz! (0.5p)
Írj egy függvényt, a neve legyen melyik_gyorsabb! A függvénynek legyen két bemenő paramétere! Az első, N, egy egész szám, a második,v pedig egy string, melynek alapértelmezett értéke legyen 'numpy'! A függvény visszatérési értéke egy másodpercben mért szám legyen. (0.25p)
A függvény visszatérési értékét az alábbiak szerint határozd meg (0.5p)!
- A numpy modul random almoduljának randn függvénye segítségével generálj két $N$ elemű véletlen számokat tartalmazó numpy.array-t, x-et és y-t ! A két array változó segítségével töltsünk fel egy harmadik array-t, z-t, úgy, hogy a z tömb i-edik eleme az x és y tömbök i-edik elemének szorzatának $\sin$-a legyen! Azaz $z_i=\sin(x_iy_i)$.
- Ha a v változó értéke 'numpy' akkor a z tömb feltöltését a numpy.array-re vonatkozó elemenkénti műveletvégzéssel, azaz for ciklus használata nélkül oldd meg!
- Ha a v változó értéke bármi más akkor a z tömb feltöltését for ciklussal oldd meg !
- Mindkét esetben a time modul segítségével mérd meg, hogy mennyi idő alatt sikerül a z tömb feltöltése! A függvényed kimenete legyen ez az idő!
Futtasd le $N=1000$ esetén a melyik_gyorsabb függvényt 2000-szer úgy, hogy v értéke 'numpy' illetve úgy is, hogy v értéke 'for ciklus'! A kapott idő értékeket tárold el két list típusú változóba (0.25p)!
Készíts egy ábrát, melyen a próbálkozások számának függvényében ábrázolod a kapott időket (0.25p)!
Készíts egy ábrát, melyen az kapott idők hisztogrammjait ábrázolod! Ehhez a matplotlib modul hist függvényét használd! A histogram elkészítésénél a bin-eket explicit add meg úgy, hogy azok logaritmikus skálán legyenek egyenletesen mintavételezve $10^{-6}$ és $10^{-1}$ között 50 pontban! A logaritmikus mintavételezést a logspace függvény segítségével gyárthatod le (0.25p).
Saját szavaiddal diszkutáld, hogy melyik eljárás a gyorsabb! (0.25p)
Fejtsd ki véleményedet 10 mondatban, azon egyénekről akik a fenti tapasztalatok ellenére a félév végéig görcsösen ragaszkodni fognak ahhoz, hogy egyszerű matematikai összefüggésekkel definiálható adatokat a numpy modul által biztosított eljárások helyett ciklusokkal töltsenek fel! (0.25p)

Feladat 3 (2.5 pont)¶

A Fibonacchi-sorozat geometriai illusztrálására sokszor alkalmazzák az alábbi ábrát:

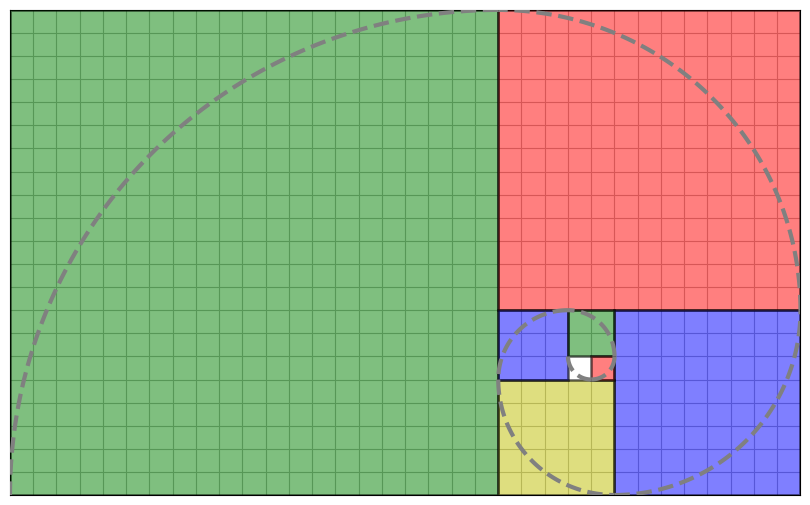
Az ábrán az egyre növekedő négyzetek oldalhossza épp a Fibonacchi-sorozat első néhány eleme szerint növekszik, azaz rendre: 1,1,2,3,5,8,13,21. A szaggatott vonal alkotta spirál struktúra pedig minden négyzetben egy megfelelő sugarú negyed körvonal. Készítsd el ezen ábrát te is a numpy és a matplotlib modulok függvényeinek segítségével (5.0p)!

Feladat 4 (2.5 pont)¶

Ebben a feladatban a numpy modul igen sokoldalú, tenzorműveletek elvégzésére alkalmas einsum függvényével fogunk megismerkedni, néhány a vektorszámítás órákon tanult fogalom segítségével. További információkért kattints ide.

Hozz létre két numpy.array-t, amelyek implementálják a Kronecker-delta és a Levi-Civita tenzorokat háromdimenziós térben. A Kronecker-delta egy kétindexű tömb, melynek diagonális elemei értéke 1, míg a többi eleme 0. A Levi-Civita egy háromindexű tömb, melynek elemei a következőképpen adódnak: (0.25p)
Az einsum függvény segítségével hozzuk létre a következő négyindexes $A$ és $B$ tenzorokat: $A_{klpq}= \varepsilon_{klm}\varepsilon_{mpq}$ és $B_{klpq}=\delta_{kp}\delta_{lq}-\delta_{kq}\delta_{lp} $! Ellenőrizzük numerikusan a mindenki számára triviális $A=B$ összefüggést a numpy modul allclose függvényével (0.5p)!
Bonyolult, több indexes tömbök egyszerű áttekintésére szolgálhat (például debuggolás céljából) ha a tömbböt kilapítjuk a flatten metódussal. Az így kapott egyindexes tömböt már egyszerűen vizualizálhatjuk, például a matplotlib modul plot függvényével. Ábrázoljuk egy ábrán az előző részfeladatban definiált $A$ és $B$ tömbök kilapított verzióját egy ábrán (0.5p)!

Móricka vektor ZH írás közben kisurran egy kétbetűs kitérőre. Az illemhely falára az alábbi kifejezést véste fel évekkel ezelőtt egy jóakarója: $$ \delta_{kl}\epsilon_{mqp}=\delta_{km}\epsilon_{lpq}+\delta_{kp}\epsilon_{mlq}+\delta_{kq}\epsilon_{mpl}. $$ Móricka nagyon megörül, mert pont kapóra jönne neki ez az összefüggés, hogy az indexes-deriválós feladatának megoldása pont kiférjen egy A0-s lapra. A feladat első részében használt módszerekkel vizsgáljuk meg, hogy vajon Móricka helyesen tette, hogy észnélkül felhasználta a fenti összefüggést!

Gyártsd le az alábbi négy tenzort (0.5p): $$ \begin{align*} C_{klmqp}&=\delta_{kl}\epsilon_{mqp} \\ X_{klmqp}&=\delta_{km}\epsilon_{lpq} \\ Y_{klmqp}&=\delta_{kp}\epsilon_{mlq} \\ Z_{klmqp}&=\delta_{kq}\epsilon_{mpl} \end{align*} $$
Készíts egy ábrát, melyen a $C$ tenzort és az $X+Y+Z$ összeg tenzort kilapítva egyszerre ábrázolod (0.5p)!
Az ábra alapjá fogalmazd meg saját szavaiddal, hogy a Móricka által használt kifejezés helyes-e. Ha nem, akkor mondd meg miért nem az (0.25p)!

Feladat 5 (2.5 pont)¶

A fizikai rendszerek szimulációja során kiemelkedő fontossággal bírnak a jól meghatározott valószínűségi eloszlások mintavételezésével előállított folyamatok vizsgálatai. Ebben a feladatban véletlen leképezések segítségével előállított ponthalmazt fogunk vizsgálni. A feladatot numpy és a scipy modulok segítségével oldd meg!

A feladat megoldásához szükség lesz adott eloszlással rendelkező véletlen egész számokra. Például vizsáljunk egy olyan véletlen számsorozatot, melyben az "1" $p_1$ valószínűséggel, a "2" $p_2$ valószínűséggel a "3" $p_3$ valószínűséggel a "4" pedig $p_4$ valószínűséggel szerepel! A feladat megoldásához a numpy modul random almoduljában található rand függvényt vehetjük igénybe. Ez a függvény olyan véletlen számokat generál a [0,1] intervallumon, amelyek egyenletes eloszlással rendelkeznek. A következőképpen járhatunk el: először generáljunk egy véletlen számot a rand függvénnyel, amit $X$-szel jelölünk. Ezt követően legyen $Y$ azon véletlen szám értéke, amelyet $X$ alapján határozunk meg. $$ Y=\begin{cases} 1 & \text{ha }X\leq p_{1}\\ 2 & \text{ha }p_{1}<X\leq p_{1}+p_{2}\\ 3 & \text{ha }p_{1}+p_{2}<X\leq p_{1}+p_{2}+p_{3}\\ 4 & \text{egyébként} \end{cases} $$ Ekkor az $Y$ véletlen szám pont a kívánt eloszlást fogja követni! Lássuk ezt be numerikusan! Az egyes számok $p_i$ valószínűségeire válasszuk az alábbi értékeket:

$i$	$p_i$
1	0.01
2	0.85
3	0.07
4	0.07

Generálj a fenti algoritmus szerint $10^3$ véletlen számot! Ezen részfeladat megoldásához NE HASZNÁLJ for CIKLUST (0.5p)!
Készítsd el a generált számok eloszlását ábrázoló hisztogramot! Erre alkalmas lehet a numpy histogram vagy a matplotlib hist függvénye (0.25p).

A feladat hátralévő részében a fenti módszerrel generált véletlen számokat fogjuk használni!

Írj egy függvényt, mely egy adott kétdimenziós $\vec{r}={\begin{bmatrix}x\\y\end{bmatrix}}$ vektoron végrehajtja az alábbi paraméteres lineáris leképezést: $$ {\displaystyle G(\vec{r})={\begin{bmatrix}a&b\\c&d\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}+{\begin{bmatrix}e\\f\end{bmatrix}}} $$ Legyen a függvény neve G és legyen két bemenő paramétere! Az első bemenő paraméter egy kétkomponensű numpy.array, mely az $\vec{r}$ vektort kódolja, a második bemenő paraméter legyen egy hatkomponensű numpy.array, mely a leképezés paraméteréül szolgáló $a,b,c,d,e$ és $f$ értékeket tartalmazza (0.5p).
Alkalmazzuk a fent definiált leképezést egymás után $10^4$-szer a $\vec{r}={\begin{bmatrix}0\\0\end{bmatrix}}$ kiindulópontból. Itt használhatsz for ciklust. Minden egyes lépésnél a leképezés paramétereit véletlenszerűen válasszuk az alábbi táblázatban közölt négy lehetséges $i=1,2,3,4$ paraméter halmaz közül, úgy, hogy a megfelelő $p_i$ valószínűséggel forduljon elő mindegyik! A kapott 10000 pont $x$ és $y$ koordinátáit tároljuk el egy numpy.array típusú változóba, például egy 10000x2-es tömbben (0.5p)!

$i$	$p_i$	$a_i$	$b_i$	$c_i$	$d_i$	$f_i$
1	0.01	0	0	0	0.16	0
2	0.85	0.85	0.04	-0.04	0.85	1.60
3	0.07	0.20	-0.26	0.23	0.22	1.60
4	0.07	-0.15	0.28	0.26	0.24	0.44

A kapott pontok segítségével készíts el négy további numpy.array típusú változót, melyek a kapott pontok transzformáltjait tartalmazzák a négy használt leképezéssel. Készíts négy ábrát, melyeken a kapott pontokat, illetve azok transzformáltjait ábrázolod(0.5p)!
A saját szavaiddal fogalmazd meg, hogy a vizsgált eljárás milyen, a közoktatásban is tárgyalt, fizikai rendszer modellezésére használható! A készített ábrák alapján tárgyald, hogy a használt négy paraméterhalmaznak milyen szerepe van (0.25p)!

Feladat 6 (2.5 pont)¶

A tridiagonális mátrixok fontos szerepet játszanak számos numerikus módszer implementálásában. Vizsgáljuk az alábbi $n\times n$-es tridiagonális mátrixot:

$$ {\displaystyle T={\begin{pmatrix}a_{1}&b_{1}\\c_{1}&a_{2}&b_{2}\\&c_{2}&\ddots &\ddots \\&&\ddots &\ddots &b_{n-1}\\&&&c_{n-1}&a_{n}\end{pmatrix}}} $$

Ezen struktúrával rendelkező mátrixok inverze zárt alakban megdható: $$ {\displaystyle (T^{-1})_{ij}={\begin{cases}(-1)^{i+j}b_{i}\cdots b_{j-1}\theta _{i-1}\phi _{j+1}/\theta _{n}&{\text{ if }}i<j\\\theta _{i-1}\phi _{j+1}/\theta _{n}&{\text{ if }}i=j\\(-1)^{i+j}c_{j}\cdots c_{i-1}\theta _{j-1}\phi _{i+1}/\theta _{n}&{\text{ if }}i>j\\\end{cases}}} $$ ahol $\theta_i$ és $\phi_i$ segédmennyiségek az alábbi rekurziós összefüggésnek tesznek eleget:

$$ {\displaystyle \theta _{i}=a_{i}\theta _{i-1}-b_{i-1}c_{i-1}\theta _{i-2}\qquad i=2,3,\ldots ,n} $$$$ \theta_0 = 1, \theta_1 = a_1 $$$$ {\displaystyle \phi _{i}=a_{i}\phi _{i+1}-b_{i}c_{i}\phi _{i+2}\qquad i=n-1,\ldots ,1} $$$$ \phi_{n+1} = 1,\quad \phi_n = a_n $$

A $T$ mátrix determinánsa is zárt alakban előáll, mégpedig a $\mathrm{det}(T)=\theta_n$ egyszerű alakban.

Hozz létre egy tridiag nevű osztályt, amely tridiagonális mátrixok tárolására alkalmas!

Az inicializáló metódus három bemenő paraméterrel rendelkezzen, melyek a főátló, illetve a felső és alsó mellékátló elemeit tartalmazza! Tároljuk ezen elemeket az a, b illetve c attribútumokban (0.25p)!
Az inicializáló rutin számolja ki a $\theta_i$ és $\phi_i$ segédmennyiségeket és tároljuk őket a th és ph attribútumokban (0.25p)!
Legyen egy inv metódus, ami két bemenő paraméterrel rendelkezik, i-vel és j-vel, melyek egész számok! A metódus visszatérési értéke a mátrix inverzének megfelelő $\left ( T\right )^{-1}_{ij}$ legyen (0.25p)!
Az osztály implementációja során külső modulok függvényeit ne használd! Amennyiben az osztály definícióban külső, például numpy, vagy scipy rutinok vannak a teljes feladatod automatikusan 0.0 pontot ér!

Az alábbi $T$ mátrix segítségével ellenőrizd implementációd megfelelő működését (0.25p):

array([[ 0,  1,  0,  0,  0],
       [-1,  1,  2,  0,  0],
       [ 0, -2,  2,  3,  0],
       [ 0,  0, -3,  3,  4],
       [ 0,  0,  0, -4,  4]])

Ekkor $T^{-1} \mathrm{det}(T)$

array([[204., -92.,  56., -24.,  24.],
       [ 92.,   0.,   0.,   0.,   0.],
       [ 56.,   0.,  28., -12.,  12.],
       [ 24.,   0.,  12.,   8.,  -8.],
       [ 24.,   0.,  12.,   8.,  15.]])

A kvantummechanikában egy $H$ Hamilton-operátor $G(z)$ Green-függvénye a következő összefüggéssel adható meg: $G(z)=\left(zI-H\right)^{-1}$. Itt $z$ egy komplex szám, $I$ pedig az egység operátor. A $z$ komplex szám általában $z=\omega+\mathrm{i}\delta$ alakban adott ahol $\delta$ egy kicsi pozitív szám. A feladat megoldása során használjuk a $\delta=0.05$ értéket!

A tridiag osztály segítségével számítsuk ki az alábbi struktúrával rendelkező Hamilton-operátor Green-függvényének elemeit! $$ {\displaystyle H={\begin{pmatrix} 0&-1\\ -1&0&-1\\ &-1&\ddots &\ddots \\&&\ddots &\ddots &-1\\&&&-1&0\end{pmatrix}}} $$ Legyen $H$ dimenziója 100!

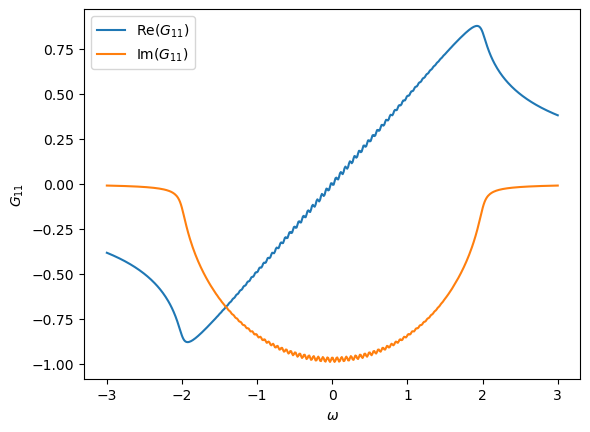
Készíts három ábrát, amelyen $\omega$ függvényében ábrázolod a Green-függvény elemeinek valós és képzetes részét. Az $\omega$ változó értékeit a $[-3,3]$ intervallumon változtassuk és legalább 500 pontban egyenletesen mintavételezzük! Az első ábra a $G_{1,1}$ a második a $G_{50,50}$ a harmadik pedig a $G_{1,100}$ elemeket ábrázolja!

Ábránként (0.5p) jár. A feladat ezen részének megoldásában már használhatod a numpy illetve a matplotlib modulok függvényeit!

Ha mindent jól csinálsz az első ábra így kell, hogy kinézzen: